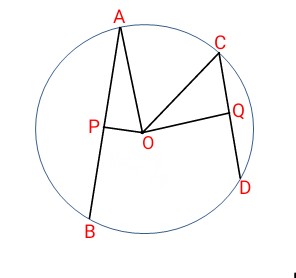
বিশেষ নির্বচনঃ ধরি, O কেন্দ্রবিশিষ্ট ACBD বৃত্তে AB, CD দুইটি জ্যা এবং AB>CD. এখন কেন্দ্র O থেকে AB ও CD এর উপর যথাক্রমে OP এবং OQ লম্ব টানা হলো যেন এরা কেন্দ্র থেকে জ্যাদ্বয়ের দুরুত্ব নির্দেশ করে।
প্রমাণ করতে হবে যে, OP<OQ
অঙ্কনঃ
A,O এবং C,O যোগ করি।
প্রমাণঃ
-
△APO এ, OP⊥AB এবং △COQ এ, OQ⊥CD। সুতরাং, △APO এবং △COQ সমকোণী ত্রিভুজ
বা, AB/2>CD/2
বা,AP>CQ
বা, AP2 > CQ2
বা, -AP2 < -CQ2
(উভয়পক্ষে -1 দ্বারা গুণ করে। উল্লেখ্য, নেগেটিভ সংখ্যা দিয়ে অসমতার উভয় পাশকে গুণ বা ভাগ করলে, অসমতার চিহ্ন পাল্টে যায়)
বা, AO2 _ AP2 < AO2 _ CQ2
(উভয়ের সাথে AO2 যোগ করে)
বা, AO2 _ AP2 < CO2 _ CQ2
(AO ও CO, একই বৃত্তের ব্যাসার্ধ)
বা, OP2 < OQ2 ( পিথাগোরাসের সূত্রানুযায়ী)
বা, OP < OQ [ প্রমাণিত ]