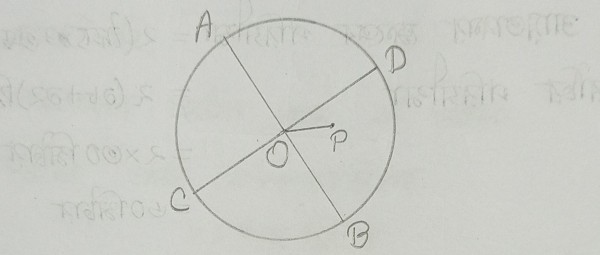
বিশেষ নির্বচন
মনে করি, ACBD বৃত্তের AB ও CD জ্যাদ্বয় পরস্পর O বিন্দুতে সমদ্বিখণ্ডিত হয়েছে। প্রমাণ করতে হবে যে, O বৃত্তটির কেন্দ্র।
প্রমাণ
১) AB ও CD পরস্পর O বিন্দুতে সমদ্বিখণ্ডিত হয়েছে।
.'. AO=OB এবং CO=OD
২) যদি O বৃত্তটির কেন্দ্র না হয়, তবে ধরি, P বিন্দু বৃত্তটির কেন্দ্র। O,P যোগ করি।
৩) AO=OB বলে PO(লম্বের চিহ্ন)AB; [বৃত্তের কেন্দ্র ও ব্যাস ভিন্ন কোনো জ্যায়ের মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যায়ের উপর লম্ব]
.'. /_POA=/_POB=এক সমকোণ... ... ... (i)
আবার,
CO=OD বলে PO(লম্বের চিহ্ন)CD ; [বৃত্তের কেন্দ্র ও ব্যাস ভিন্ন কোনো জ্যায়ের মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যায়ের উপর লম্ব]
.'. /_POD=/_POC=এক সমকোণ... ... ... (ii)
৪) (i) ও (ii) তুলনা করে পাই,
/_POA =/_POD=এক সমকোণ
কিন্তু তা অসম্ভব। কারণ /_POD, /_POA এর অংশ।
.'. P বৃত্তটির কেন্দ্র হতে পারে না।
সুতরাং, O বিন্দুটিই বৃত্তটির কেন্দ্র।
(প্রমাণিত)